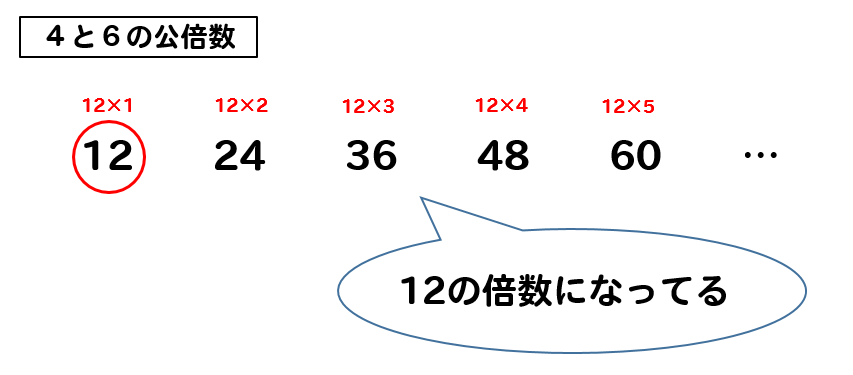
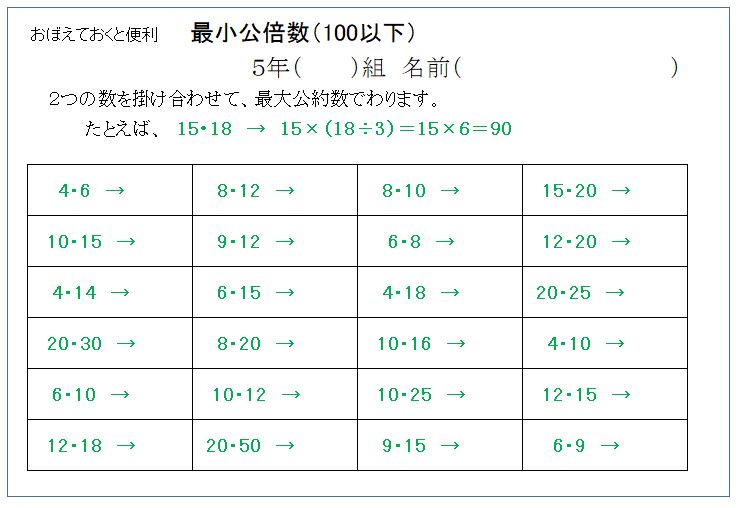
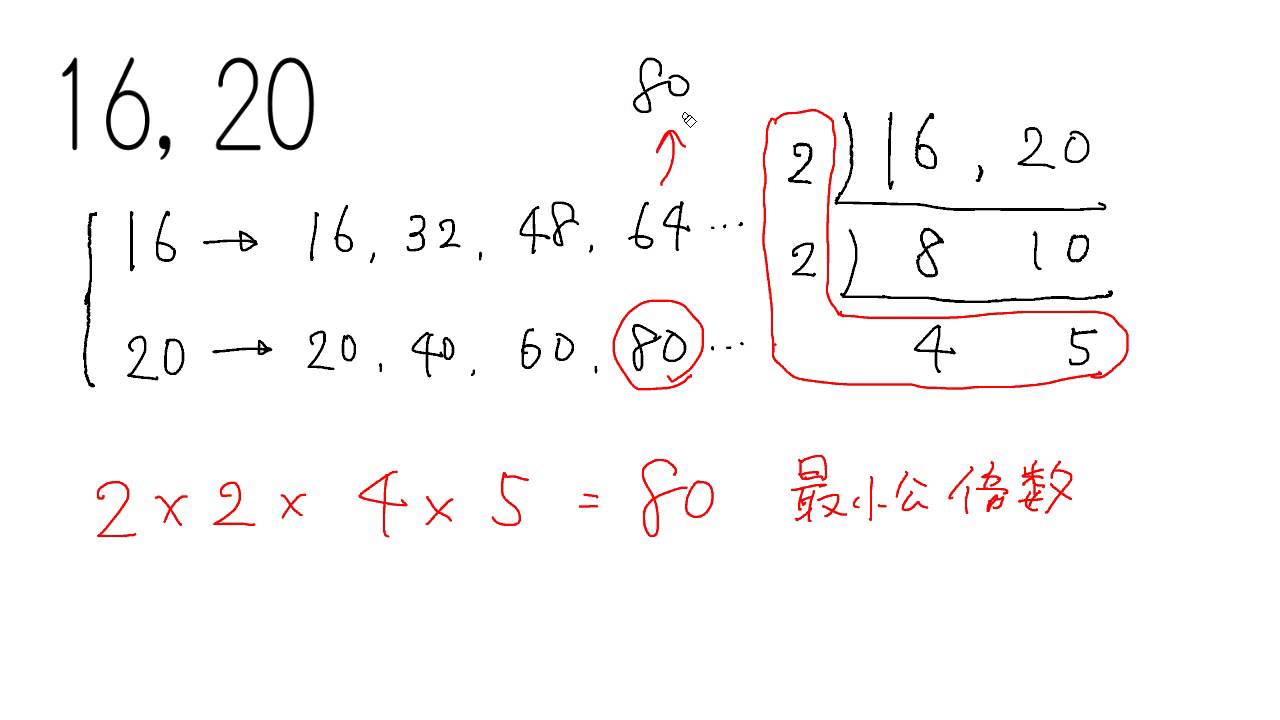
公倍数を求めるには、最小公倍数を求めればよいことがわかりました。 では、その最小公倍数は、どのようにすれば求められるのでしょうか? 2と3、4と5のように、2つ以上の数すべてを割り切れる数が1だけの場合、これらの数を「 互いに素(そ) 」といいます。 互いに素の数同士では、それらの数をかけた数が最小公倍数になります。 たとえば、2と3の最小公倍数は2×3=6、4
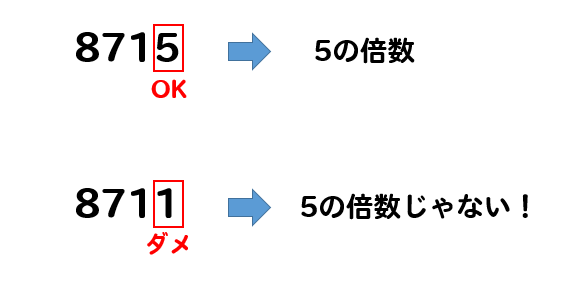
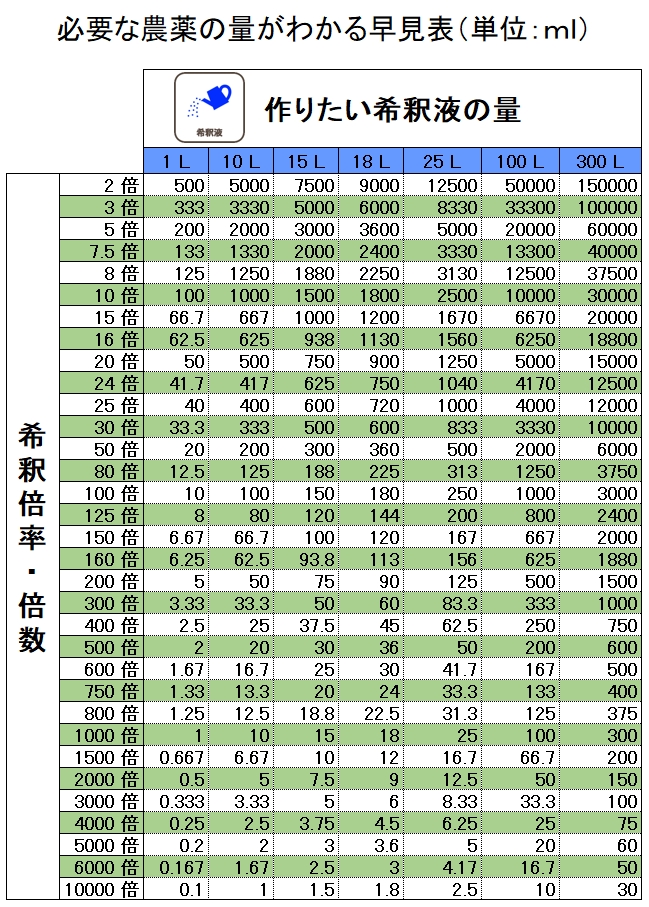
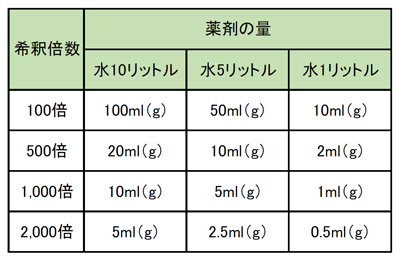
倍数 の 求め 方-原液の量 = 水量 ÷ (希釈倍率 - 1) 「水量」も「希釈倍率」も決まっていますので、後は当てはめるだけ。 計算の考え方 この計算をする時にも、大前提として「2倍希釈」や「3倍希釈」を理解しておく必要があります。 ここでは分かりやすいように「3倍希釈」を例にして、この計算式で答えが出る理由を説明します。 繰り返しになりますが、「3倍希釈」とは「"原液の3倍"の溶液(希釈液)を作る 素数の見つけ方の例を2つ紹介しますが、①はテストのときなどでも活用できるでしょう。 素数を見つける方法①:消去法で倍数や偶数を削る 一の位に着目 →0・2・4・6・8:偶数(2の倍数)のため除外 →5:5の倍数のため除外 各位の数字を足す
倍数 の 求め 方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「倍数 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「倍数 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「倍数 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「倍数 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「倍数 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
 |  | |
「倍数 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「倍数 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「倍数 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |
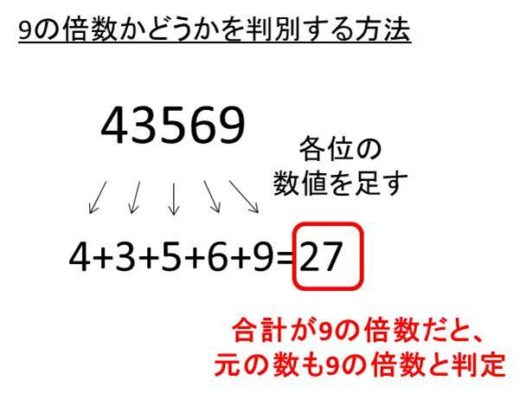
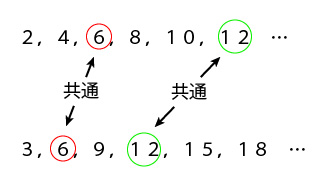
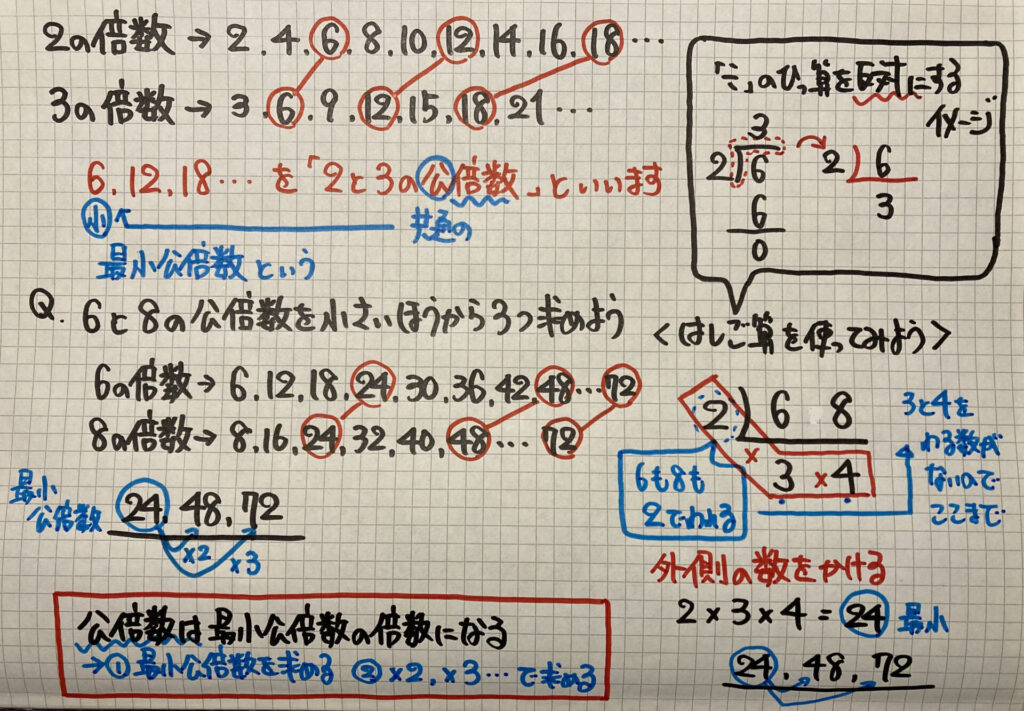
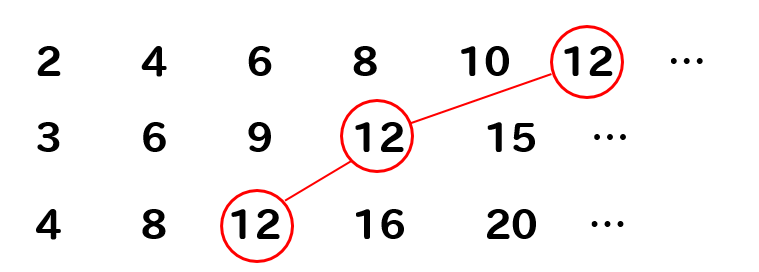
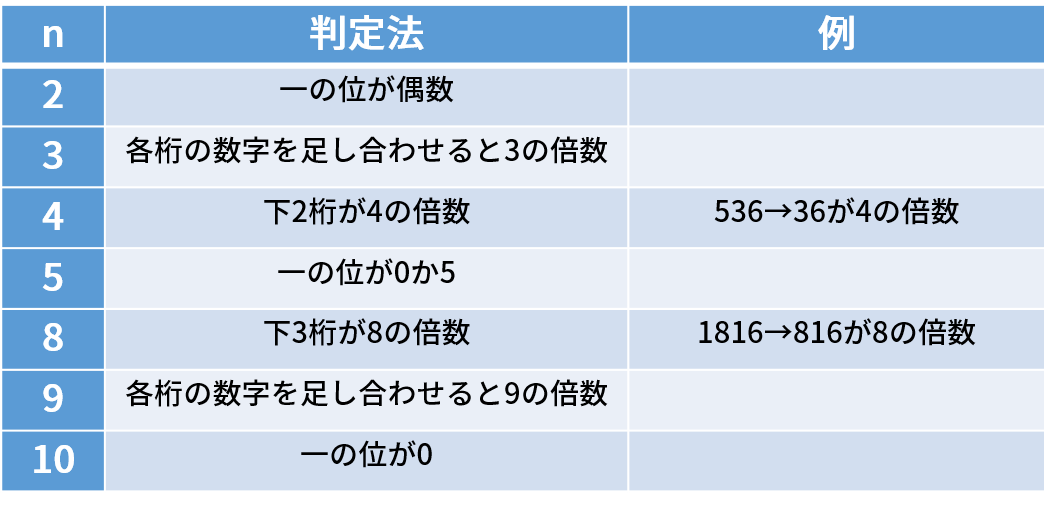
2の倍数 かつ 3の倍数であれば、6の倍数である。 2の倍数 → 1の位が、 0か、2の倍数 (2,4,6,8) であれば、その数字は 2の倍数 3の倍数 → 各位の 数字の和が 3の倍数 であれば、その数字は 3の倍数 例) は、1の位の数 が 6 (2の倍数) なので 2の倍数 は、 Link 超かんたん!!3の倍数の見つけ方 の法則を使って、 3の倍数 よって、 は、 2の倍数 かつ 3の 入試の倍率の求め方を教えてください 受験者数(例250人) 合格者数(0人)=倍率(125倍)試験前が予定倍率、試験後が確定倍率になります。また、合格者数×(倍率 1)=不合格者数




